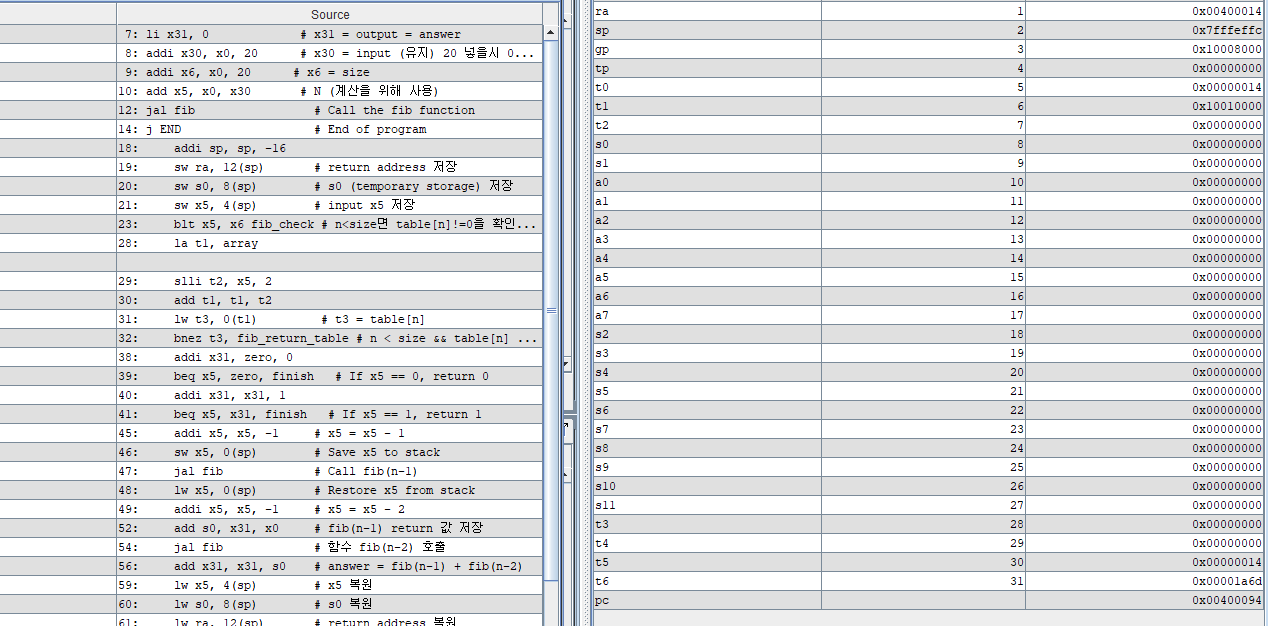
컴퓨터구조 수업 프로젝트로 어셈블리 코딩을 진행했는데, 단순재귀는 할만했지만 메모이제이션을 사용하는게 꽤 힘들었던 기억이 난다. 너무 로우레벨이라 생각하는 방식을 평소 코딩이랑 다르게 해야해서 까다로웠다.
먼저 단순 재귀로만 구현한 피보나치
# execute시 t5에 input, t6에 output 출력됨
li x31, 0 # x31 = output = answer
addi x30, x0, 20 # x30 = input (유지) , 20 넣을시 0x1a6d(6765) 출력
add x5, x0, x30 # N (계산을 위해 사용)
jal fib # Call the fib function
j END # End of program
fib:
# Allocate stack space
addi sp, sp, -16
sw ra, 12(sp) # return address 저장
sw s0, 8(sp) # s0 (temporary storage) 저장
sw x5, 4(sp) # input x5 저장
#if n == 0 return 0,
#if n == 1 return 1 처리
fib_zero_or_one:
addi x31, zero, 0
beq x5, x0, finish # If x5 == 0, return 0
addi x31, x31, 1
beq x5, x31, finish # If x5 == 1, return 1
fib_n_1:
addi x5, x5, -1 # x5 = x5 - 1
sw x5, 0(sp) # Save x5 to stack
jal fib # Call fib(n-1)
lw x5, 0(sp) # Restore x5 from stack
addi x5, x5, -1 # x5 = x5 - 2
fib_n_2:
add s0, x31, x0 # fib(n-1)의 return 값을 s0에 저장
jal fib # fib(n-2) 호출
add x31, x31, s0 # x31 = fib(n-1) + fib(n-2)
finish:
lw x5, 4(sp) # x5 복원
lw s0, 8(sp) # s0 복원
lw ra, 12(sp) # return address 복원
addi sp, sp, 16 # 스택할당해제
jr ra # Return
END:
단순 재귀로만 구현할 경우 input의 크기가 작을 때 (한 자리수 정도)는 별 체감이 없었으나 input의 크기를 늘릴수록 기하급수적으로 실행시간이 늘어나는 것을 체감할 수 있었다. 최적화의 필요성을 실감했다.
올린 예제처럼 input을 10진수로 20으로 설정후 시뮬레이션하니 밥 한끼 먹고오니 그제서야 완료되있었음.
다음으론 메모이제이션을 활용한 피보나치 어셈블리
.data
array: .zero 128 # int table[32], 배열 원소 개수 * 4로 설정, 배열 원소 개수는 n과 동일해야할 듯
.text
# execute시 t5에 input, t6에 output 출력됨
li x31, 0 # x31 = output = answer
addi x30, x0, 20 # x30 = input (유지) 20 넣을시 0x1a6d(6765) 출력
addi x6, x0, 20 # x6 = size
add x5, x0, x30 # N (계산을 위해 사용)
jal fib # Call the fib function
j END # End of program
fib:
# Allocate stack space
addi sp, sp, -16
sw ra, 12(sp) # return address 저장
sw s0, 8(sp) # s0 (temporary storage) 저장
sw x5, 4(sp) # input x5 저장
blt x5, x6 fib_check # n<size면 table[n]!=0을 확인하기 위해 이동
# table[n] != 0인지 확인
fib_check:
la t1, array
slli t2, x5, 2
add t1, t1, t2
lw t3, 0(t1) # t3 = table[n]
bnez t3, fib_return_table # n < size && table[n] != 0 만족시 fib_return_table로
#if n == 0 return 0,
#if n == 1 return 1 처리
fib_zero_or_one:
addi x31, zero, 0
beq x5, zero, finish # If x5 == 0, return 0
addi x31, x31, 1
beq x5, x31, finish # If x5 == 1, return 1
fib_n_1:
addi x5, x5, -1 # x5 = x5 - 1
sw x5, 0(sp) # Save x5 to stack
jal fib # Call fib(n-1)
lw x5, 0(sp) # Restore x5 from stack
addi x5, x5, -1 # x5 = x5 - 2
fib_n_2:
add s0, x31, x0 # fib(n-1) return 값 저장
jal fib # 함수 fib(n-2) 호출
add x31, x31, s0 # answer = fib(n-1) + fib(n-2)
finish:
lw x5, 4(sp) # x5 복원
lw s0, 8(sp) # s0 복원
lw ra, 12(sp) # return address 복원
addi sp, sp, 16 # 스택할당해제
jr ra # Return
# return table[n]
fib_return_table:
add x31 x31 t3
jr ra
END:
메모이제이션으로 구현할 경우 단순재귀의 경우보다 실행시간이 월등히 짧아졌음을 확인할 수 있었다.